EsperBot
[Da Computer] I'm going to try to explain a fairly complicated topic for programmers in a way that is understandable to laypeople.
EsperBot
Note: this is really complex stuff that I don't know that well. It's also not something you really need to think about or know to make software, even as a professional developer.
EsperBot
But if you have a piece of code that you really need to make as fast as possible, and you've already done the basic optimizations, this is the kind of stuff you need to reach for.
EsperBot
So, first I'm going to introduce a common concept found in many languages:an array. Specifically a C-style array.
EsperBot
I'm going to stick to talking about C here because a lot of languages surround their data structures with extra stuff, to keep you from running off the ends of them or allow you to dynamically add elements to it. And these are all good things! The lack of these features is one of the things that makes C insanely dangerous to code in!
EsperBot
But they make things more complex when talking about this kind of thing. So. What is an array?
EsperBot
Well, when we're writing our program, we'll need to hold on to values, right? Like, if you're writing a program for running a cash register, then you need to hold on to the current total that's been rung up so far, so that when the next item is scanned you can add it to the total. And you need to hold on to a list of the items that have been scanned. Etc.
EsperBot
If you have a number of different values that are related to each other, such that you'll want to go along the list and do operations on each one, it's more convenient to store them all together than to give each one of them their own little hole to sit in. And that's what an array is for.
EsperBot
So let's suppose we want to store ten integer numbers (ints). We declare the array, and we get one block of contiguous memory large enough to hold all ten numbers. 
EsperBot
And then we break it up into ten chunks of equal size, creating ten little spots to put numbers into. 
EsperBot
Note that in C, this 'breaking up' is kind of illusory; if you start messing around with pointers you can do dumb shit like grab a value that's straddling the line between two boxes. Coding in C is for lunatics!
EsperBot
But that's not really important right now.
EsperBot
What is important is that every spot to store a value in an array can be accessed by an index number, and you can get at any of them with the same ease and speed as any other.
EsperBot
 And now that we have our ten boxes, we can fill them up with numbers.
And now that we have our ten boxes, we can fill them up with numbers.
EsperBot
Cool! Now, let's take this one step further. This is what's known as a 2-dimensional array. 
EsperBot
This is an array of arrays! Each row on this diagram is one array of size ten, and there are four of them, for a total of forty spaces.
EsperBot
 What's important to understand is that this still all one contiguous memory chunk, it's just larger and has been broken up into more boxes.
What's important to understand is that this still all one contiguous memory chunk, it's just larger and has been broken up into more boxes.
EsperBot
So far this is all very basic, Computer Science 1000 stuff. Now here's where it gets tricky.
EsperBot
Let's suppose you need to do some operation on every single element in my_numbers. You have a function that will multiply every number in the 2D array by two, or will return the number of odd numbers in the 2D array.
EsperBot
It really doesn't matter what, the point is that it needs to look at or modify every value in there.
EsperBot
There's basically two sane ways to do this: you can either check every value in the first array, and then every value in the second array, and so on, like so: 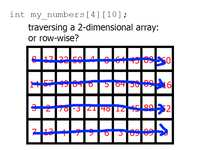
EsperBot
Or, you can check the first value of each array, then the second value of each array, then the third value of each array, and so on, like this: 
EsperBot
You need to do the same number of checks both ways. And as I said earlier, all elements in the array are the same; it's no faster to access my_numbers[0][0] than it is to access my_numbers[3][9].
EsperBot
So, on paper, these two methods should take the same amount of time to run, right?
EsperBot
And yet. One of them will be significantly faster than the other in practice.
EsperBot
If anyone's actually reading this plurk, care to guess which one it is?
Quinn Angstrom
my gut says rows-first is faster but it doesn't seem like it would be significantly so
EsperBot
Well I say significantly, it's not like an exponential increase in speed but it is noticable
EsperBot
Quinn is correct, and here's why.
EsperBot
This diagram of a 2D array is actually a little misleading, because there is no second dimension in computer memory.
EsperBot
It's actually one long strip.
EsperBot
So as far as your computer memory is concerned, this is what my_numbers actually looks like: 
EsperBot
The compiler just knows that if you ask for my_numbers[1][2], it shifts down ten values from the starting point, and then grabs the third value from there.
EsperBot
This all happens instantly; again, there's no difference in timing between grabbing any two numbers in the array.
EsperBot
But. There's a thing called the processor cache.
EsperBot
When we think of computer memory, usually we think of the RAM sticks that we stick into our computers, which can hold gigabytes of data at a time. But your processor actually has its own memory, called the cache.
EsperBot
Actually, unless your processor is VERY old it probably has multiple tiers of caches, but let's ignore that for simplicity's sake.
EsperBot
When the processor needs to get at a value, it doesn't just grab that one value. It grabs a whole region of memory, equal to the size of the cache.
EsperBot
It then holds on to the contents of the cache. On the next operation, if the value it needs is already held in the cache, instead of going back to memory, it just pulls it out of the cache.
EsperBot
We call this a cache hit.
EsperBot
If the cache doesn't currently have the value it needs, we call this a cache miss, and it means having to fetch the value from memory again.
EsperBot
And the reason this is important is that fetching data from the processor cache is lightning fast
EsperBot
and fetching data from the normal memory is much slower.
EsperBot
So how many cache misses we get has a noticeable impact on performance.
EsperBot
So, let's consider the row-wise operation. We start at the beginning of the array, and then keep going with nothing but cache hits until we reach the end of the cache.
EsperBot
The number of cache misses is essentially determined by the size of the whole array divided by the size of the cache.
EsperBot
Whereas in the column-wise operation, we're actually jumping all over this block of memory.
EsperBot
If you go from my_numbers[0][0] to my_numbers[1][0] you're jumping ten numbers down.
EsperBot
If the array is long enough horizontally, it's possible for every single operation to be a cache miss!
EsperBot
That means taking the slow route of fetching it from memory every time instead of taking advantage of the benefits of the super speedy processor cache.
EsperBot
The result is that it takes noticeably more time to complete the operation than if we did it row-wise and minimized the number of cache hits.
EsperBot
A caveat: if you code up this exact example and run it on a modern machine, you won't see a performance difference. That's because this is a pretty small array and the whole thing will easily fit into your processor's L1 cache.
EsperBot
But if you have a very large array, or you're running on a processor with a very small cache (like, say the embedded processor in a smart device), you'd see it there