Arbieroo
(a^x)^y does not equal a^(x^y)...
Arbieroo
...and if you do it the wrong way in your algorithm you do not get the pretty fractal you hoped for...
🌸wotitdo🌸
please excuse my dear aunt Sally
Arbieroo
🌸wotitdo🌸
: for what? I mean, if she's a neo-Nazi, crypto-fascist scumbag who eats manatees for breakfast, I'm not excusing any Sally, regardless of whose aunt she might be! 
🌸wotitdo🌸

Arbieroo

JigmeDatse
if there's a connection between the crypto-fascists and the crypto-bros.
Arbieroo
not aware of the crypto-bros, so I really don't know 
JigmeDatse
there is a connection. Crypto-bros are the people who promote cryptocurrency and other block chain related technologies (none of which I've seen as being good).
Arbieroo
they're probably self-serving sociopaths, then, but not necessarily cyrto-fascist.
Arbieroo
so here's the fractal:
Arbieroo
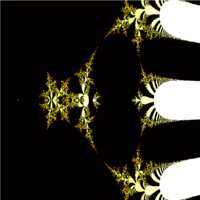
sef_lopod
not done that one (as far as I recall).
Arbieroo
imagine Z^Z^Z^... where Z is complex. As for the Mandelbrot set, a starting value of Z might, after some number of iterations, go to a constant value, enter a cycle of some number of steps or "escape" to infinity.
Arbieroo
here, starting values of Z that remain finite are coloured black (as is typical for the Mandelbrot set). Other colours all escape, the brighter the colour the faster they do so.
Arbieroo
for the Mandelbrot set, |Z| > 4 is proven to escape to infinity, so you can check for that condition and curtail your iterations accordingly. In this case, I have not been able to find any analogous threshold being referred to. (I haven't checked the technical literature).
Arbieroo
that should be |Z|^2 > 4 or |Z| > 2.
Arbieroo
in the image, the real axis is along the horizontal line of mirror symmetry.
Arbieroo
the imaginary axisis harder to locate: The origin is to the left of the two large central overlapping ovals (black). There's a structure that looks like a crab facing viewer's right, seen from above. It seems to be holding a smaller version of itself. The Origin is in the "head" of the "crab".
Lemongrass
Maths Makes Monster Crabs 
Arbieroo
Lemongrass
: 
Arbieroo
they don't seem that monstrous to me, though.