Quinn Angstrom
[math] the diagonalization proof, in its basic form. because I'm a nerd who likes both math and explaining things
Quinn Angstrom
/fixes OP
Quinn Angstrom
so diagonalization proofs are a whole category of proofs, that deal with the concept of different kinds of infinity
Quinn Angstrom
there are, to ignore some esoteric weirdo shit, two kinds of infinite
Quinn Angstrom
countable infinities, and uncountable infinities
Quinn Angstrom
a set is countably infinite if you can order all of the things into an infinitely-long list
Quinn Angstrom
for example, the set of all positive integers is countably infinite
Quinn Angstrom
1, 2, 3, 4, 5, etc
Quinn Angstrom
the set of all integers is also countably infinite
Quinn Angstrom
you could list them like 0, 1, -1, 2, -2, 3, -3, etc
Quinn Angstrom
an infinitely long list, but a predictable list that eventually contains any integer
Quinn Angstrom
uncountable infinites are sets so infinite that they can't be put in any list, even an infinitely long list
Quinn Angstrom
the set of all numbers is uncountably infinite. not just integers, all of the ones in between
Quinn Angstrom
the set of all numbers between 0 and 1 is uncountably infinite
Quinn Angstrom
and that is what we're here to prove
Quinn Angstrom
it's possible to kind of think of a way you might order a list of all numbers between 0 and 1
Quinn Angstrom
maybe start with 0.0, 0.1, 0.2, etc up to 0.9, then 0.11, 0.12, 0.13, etc
Quinn Angstrom
or go 0.5, then cut each half of that in half to get 0.25 and 0.75, then halve each of those, etc
Quinn Angstrom
that'd give you a list of numbers that looks like this
that'd give you a list of numbers that looks like this
Quinn Angstrom
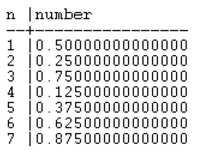actually let's do this one
actually let's do this one
Quinn Angstrom
skips 0 but whatever
Quinn Angstrom
works better for my example
Quinn Angstrom
so given this list
Quinn Angstrom
I can create a number that I can prove does not exist anywhere in the list
Quinn Angstrom
how I make it:
Quinn Angstrom
take the diagonal
take the diagonal
Quinn Angstrom
increase each digit by 1
Quinn Angstrom
if it's a 9, roll it around to 0
Quinn Angstrom
and you get this new number
and you get this new number
Quinn Angstrom
where is it in the list?
Quinn Angstrom
it's not in slot 1 - the 1st digit is off by 1
Quinn Angstrom
it's not in slot 2 - the 2nd digit is off by 1
Quinn Angstrom
it's not in slot X - the Xth digit is off by 1
Quinn Angstrom
every number on the list is guaranteed to be at least one digit off from the new number
Quinn Angstrom
proving that the number is not on the list
Quinn Angstrom
and you could try to fix this
Quinn Angstrom
by making this mystery number the 1st number on the list, then moving all the others down 1
Quinn Angstrom
like so
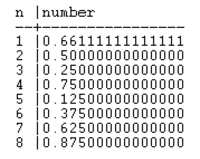like so
Quinn Angstrom
but this is futile
Quinn Angstrom
because you can just do it again
Quinn Angstrom
take the diagonal of the new list, offset each digit
Quinn Angstrom
you've got a new number that isn't on the list
Quinn Angstrom
no matter what the content of the list is, you can create a number that isn't on the list
Quinn Angstrom
therefore, real numbers are uncountable
Quinn Angstrom
they can't be comprehensively listed
Quinn Angstrom
you can expand this proof to prove things like the existence of functions that can't be expressed in any programming language
Echo
Neat. : D